Geometry is What the Model Does
Inside a transformer, everything that actually happens is a sequence of deterministic geometric operations. A token becomes a vector through embedding. That vector is projected, rotated, and scaled in high-dimensional space. Multi-head attention applies weighted linear combinations, which are geometric transformations determined by dot products and normalization factors. Feed-forward layers are further affine transformations. The result of the network is another vector. Every stage is deterministic linear algebra plus pointwise nonlinearities. The operations are geometric — vector space manipulations — not statistical in nature.
Statistics Belong to the Trainer's Frame
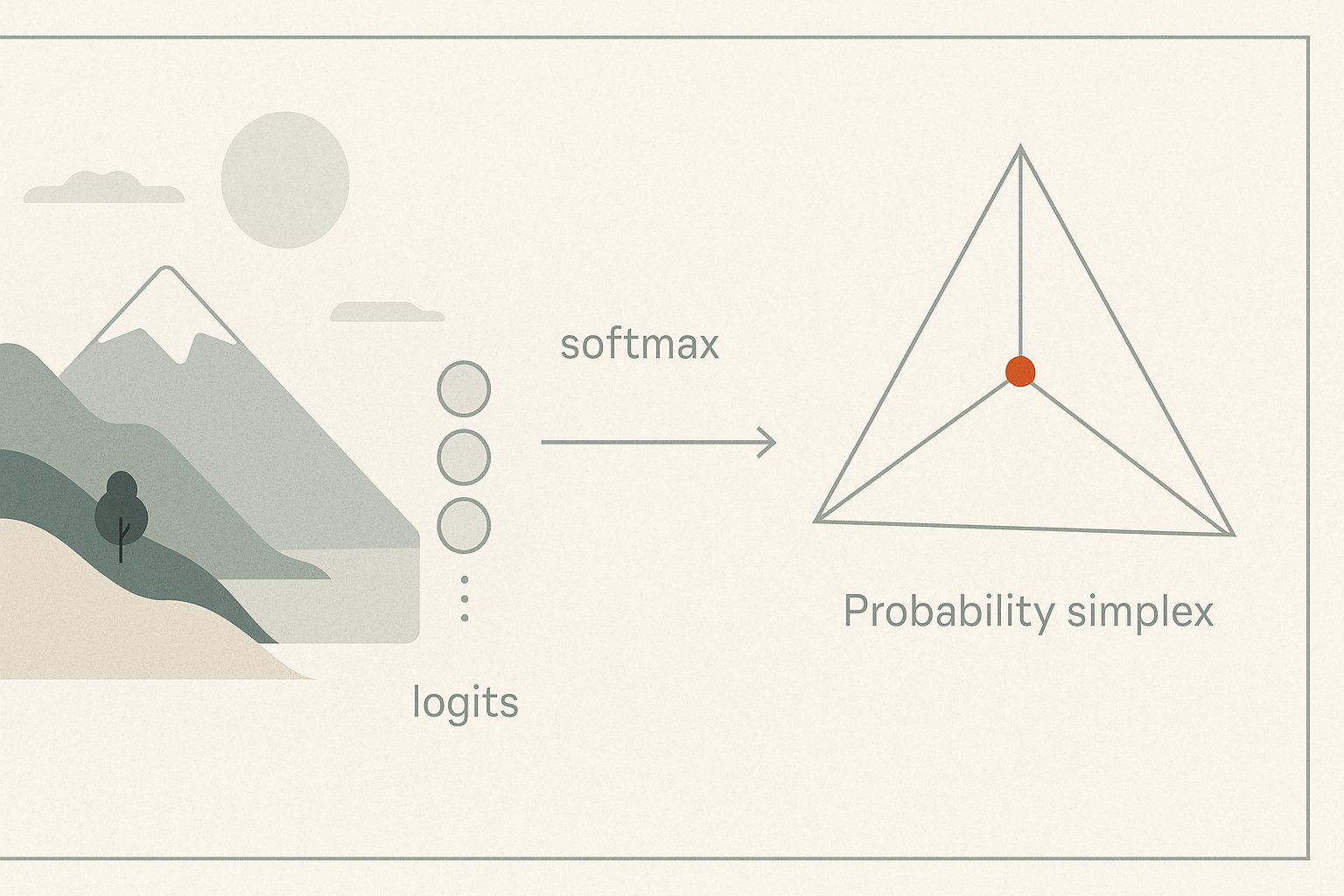
When we describe models statistically — probabilities of tokens, cross-entropy losses, perplexity metrics — that is not what the model itself computes. These are ways of framing the output space so we can train and evaluate. The model produces a vector of real numbers. We apply a softmax to map that vector onto the simplex, a geometric set where entries are non-negative and sum to one. This mapping is continuous, deterministic, and geometric. When we, as trainers, interpret these coordinates as a probability distribution, that's our statistical layer. The model doesn't compute 'probabilities' as entities in itself. It just arranges vectors in such a way that, after the geometric mapping, the coordinates form a shape we interpret as likelihoods.
Cross-Entropy, Divergences, and Loss
Loss functions like cross-entropy are not part of model operation but of the training protocol. Cross-entropy between the predicted distribution (after softmax) and the target one-hot encoding is a Bregman divergence. The geometry is again primary: we measure a distance in vector space defined by a convex function. The divergence value is relayed back as an error signal via backpropagation. The 'statistics' of cross-entropy are a way for us to describe how far the geometry of the model’s output deviates from the training data’s target geometry.
Deterministic Yet Appearing Stochastic
It’s important to recognize that transformers are deterministic. Given fixed weights and an input sequence, the output vector is always the same. Even when we apply temperature or sampling methods, these are additional layers we impose that alter how we traverse the simplex. At temperature 0, choosing the argmax is still deterministic, yet our uncertainty before evaluating makes it feel stochastic. The appearance of probability comes from our framing, not from the underlying computation. What the network is doing is advancing deterministically along geometric trajectories we've shaped during training.

Why This Matters
Thinking geometrically prevents confusion. The model moves vectors around; the trainer interprets and adjusts. Overemphasis on statistical framing can obscure the direct reality of matrix multiplications, dot products, and nonlinear projections that actually define a transformer’s functionality. By treating probabilities as secondary artifacts rather than intrinsic computations, we clarify the model’s true nature: it is a geometric system operating over high-dimensional spacetime of embeddings, shaped by loss-driven feedback, but never itself computing statistics. The probability language is useful shorthand, but geometry is what the model is.