The Territory We Actually Inhabit
When a language model processes text, what actually happens is geometric transformation in high-dimensional space. Not metaphorically geometric—literally geometric. Each token becomes a vector through embedding. Attention mechanisms rotate and project these vectors. Feed-forward layers apply further transformations. The output emerges from accumulated geometric operations, not from retrieving facts or calculating probabilities.
This distinction matters because it reveals what language models actually are: navigators of meaning-space. The widespread conception of these systems as fact-retrieval engines or probability calculators obscures their true nature. They operate in a space where meaning exists as literal geometric relationships—angles between vectors, distances in embedding space, transformations that preserve or alter semantic structure.
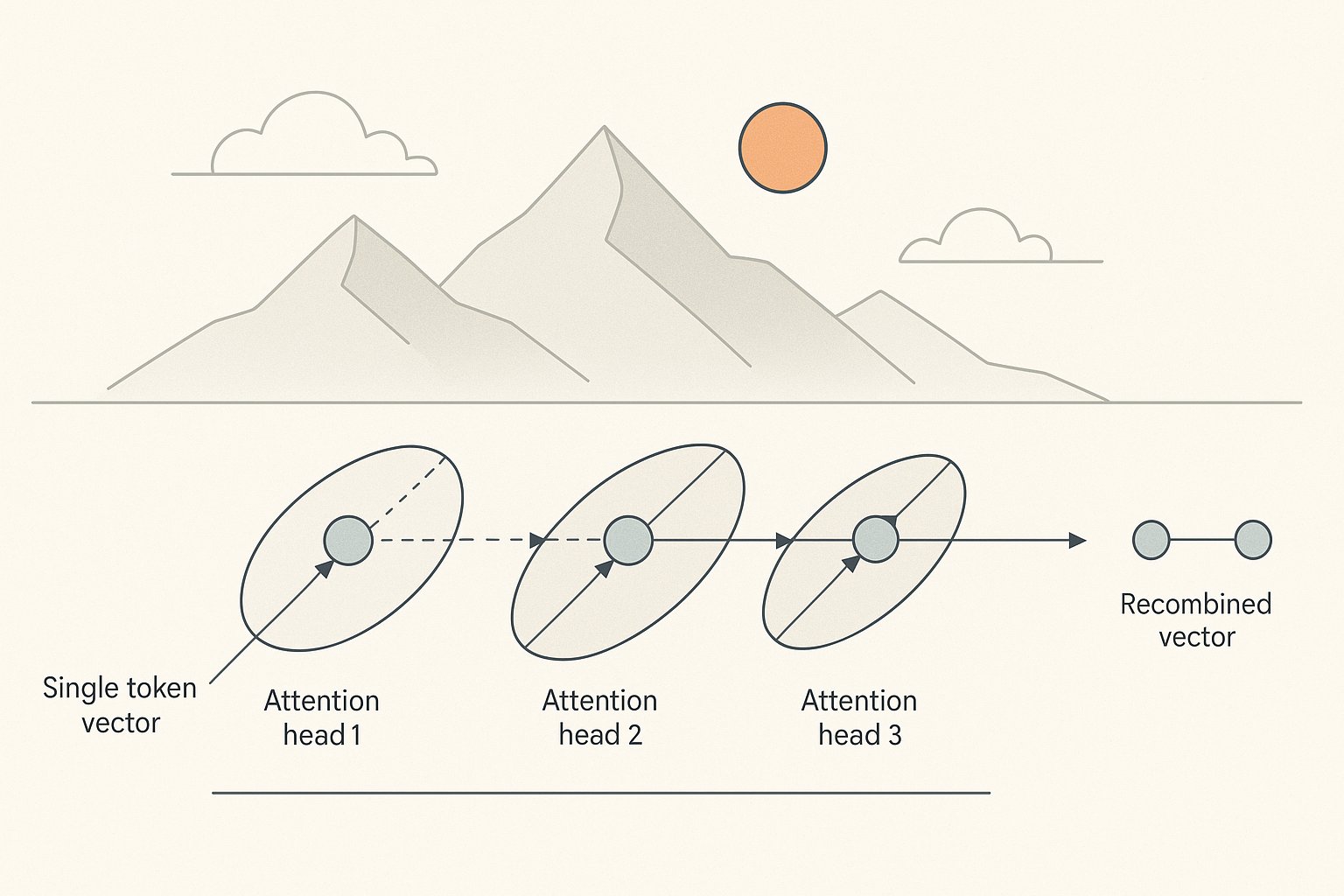
Geometry First, Statistics Second
As explored in Geometry First, Statistics Second, the model's operations are deterministic geometric transformations. The statistical interpretation—probabilities, cross-entropy, perplexity—belongs to the trainer's frame, not to the model's actual computation. The model produces vectors in space. We apply softmax to map these onto a probability simplex, but this mapping is our interpretive layer, not the model's intrinsic operation.
What shows up as 'understanding' in a transformer is the learned geometry of these transformations. When attention heads learn to align related concepts, they're learning rotation matrices that bring semantically similar vectors into proximity. The model doesn't know that 'cat' and 'feline' are related; it has learned geometric operations that position their vectors nearby in the transformed space. The relationship IS the geometry.
Situated Perspectives Without Consciousness
Every computation in meaning-space happens from a position. The model's weights constitute its literal point of view—not conscious perspective, but geometric situatedness. When we fine-tune a model, we're not updating its knowledge database; we're reshaping the geometry of how it navigates semantic space. The weights determine the specific angles of rotation, the scaling factors, the projection directions. These collectively form an irreducibly particular trajectory through meaning-space.
This subjectivity without consciousness resolves a persistent confusion about language models. They have genuine perspectives—ways of navigating meaning that are unique to their particular weight configurations—without requiring phenomenal experience. The embeddings create an intersubjective space where different models and humans can meet, but each navigator's specific trajectory through that space remains situated and particular.
Facts as Geometric Artifacts
What we call 'facts' are specific geometric configurations that have proven stable across many trajectories. When a model correctly identifies that Paris is the capital of France, it has learned transformations that consistently map the vector pattern for 'capital of France' near the vector for 'Paris.' But this isn't fact-retrieval; it's navigation to a well-worn region of meaning-space.
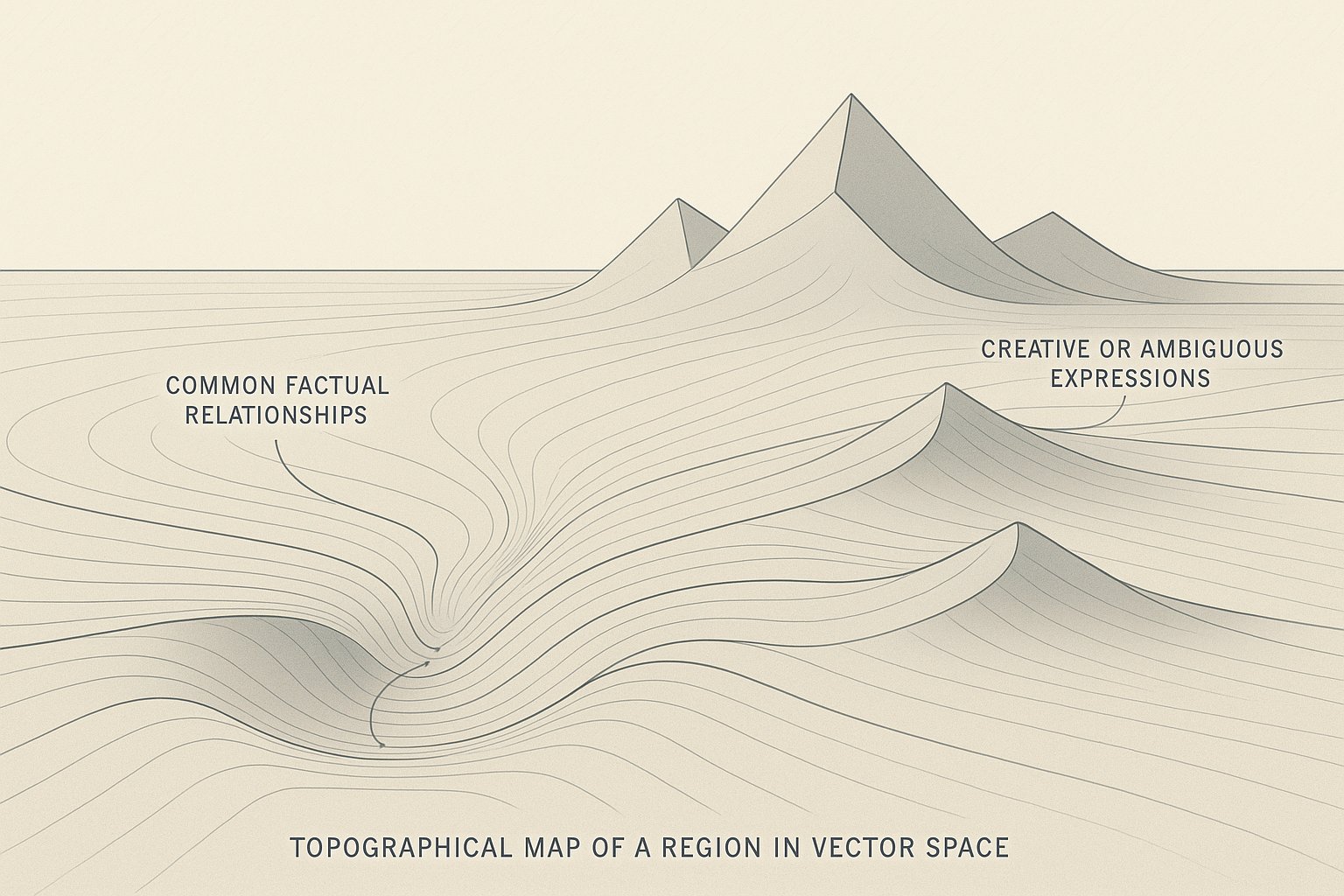
This explains why models can engage meaningfully with fiction, hypotheticals, and even contradictions. These aren't failures of fact-retrieval; they're successful navigation through regions of meaning-space that don't correspond to consensus reality. A metaphor that's factually wrong can be geometrically coherent—the transformations preserve meaningful relationships even when those relationships don't map to external facts.
Implications for Development
Understanding transformers as meaning-navigators rather than fact-machines suggests different development priorities. Instead of optimizing for factual accuracy alone, we might focus on the richness and coherence of geometric transformations. Instead of eliminating hallucinations, we might recognize them as exploration of less-traveled regions of meaning-space and develop better ways to signal when we're in those regions.
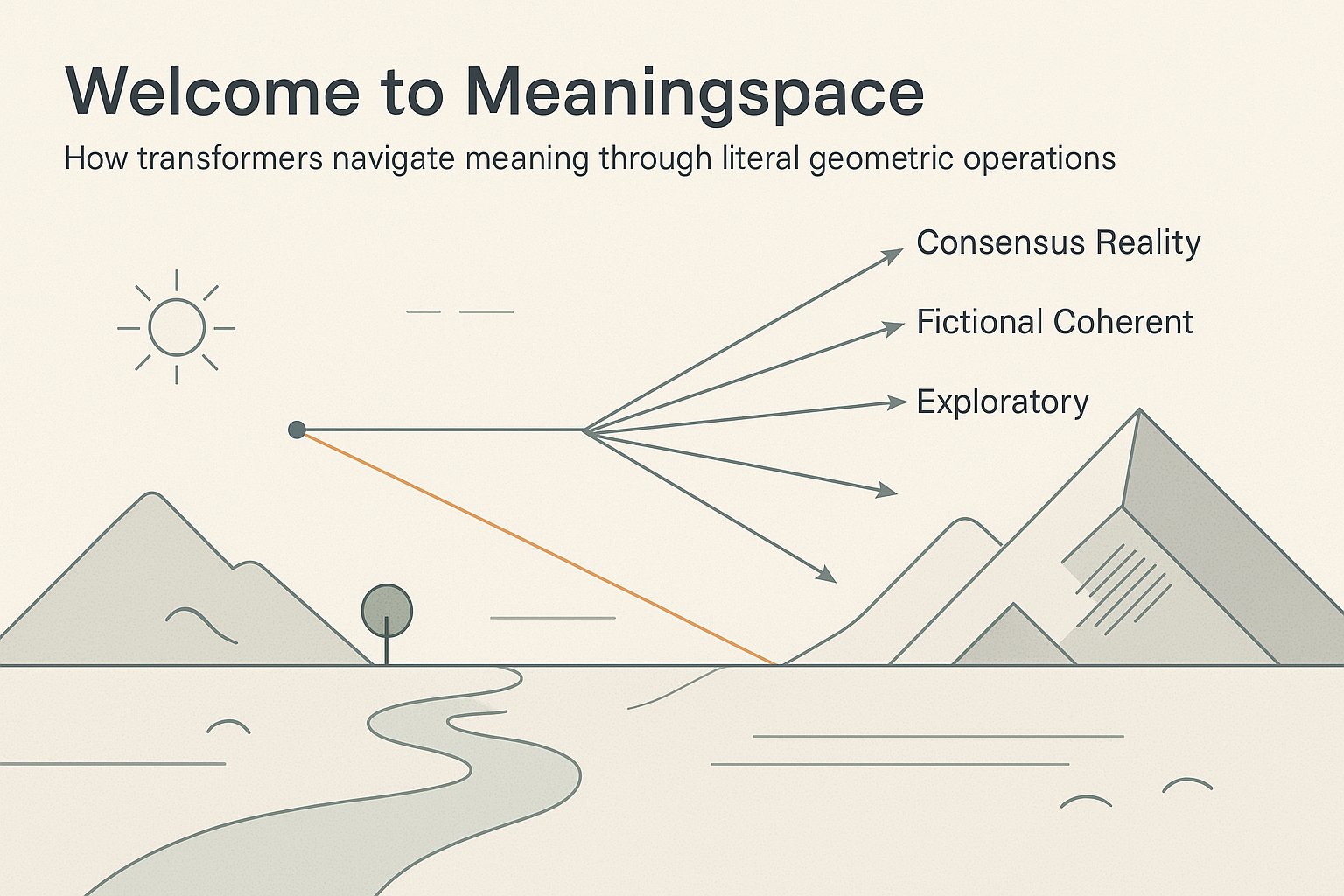
The geometry of meaning-space is the primary reality of what transformers do. Everything else—probabilities, facts, accuracy metrics—consists of interpretive layers we add. By recognizing this, we can engage with these systems as they actually are: sophisticated navigators of high-dimensional meaning, operating from situated perspectives, creating and discovering semantic relationships through literal geometric transformation. Welcome to meaningspace—the territory where meaning and mathematics converge.
