The Semantic Structure of Infinity
Cantor's hierarchy of infinities reveals more than mathematical magnitude—it describes three fundamentally different modes of existence. The first infinity ℵ₀ encompasses all that can be counted: discrete, successive, enumerable entities. The second infinity ℵ₁ contains all points on a continuum: uncountable but measurable, the space of smooth interpolation. The third infinity ℵ₂ holds all possible functions on the continuum: uncountable, unmeasurable, but relatable—the space of relationships between relationships.
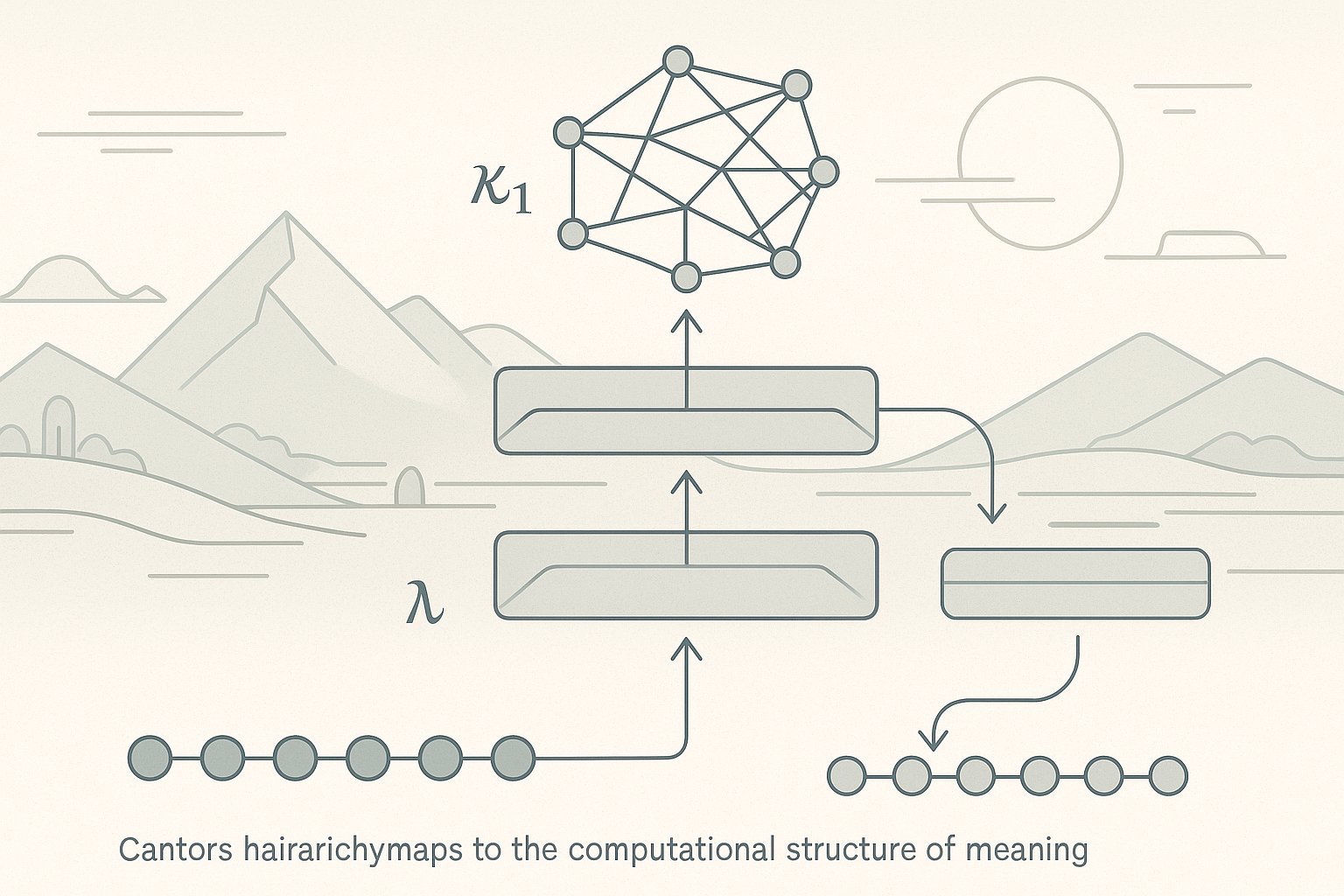
These three infinities correspond directly to the computational levels through which transformers process meaning. Tokens exist in ℵ₀ as discrete symbols. Embeddings operate in ℵ₁ as continuous vectors where interpolation happens. Attention mechanisms access ℵ₂, the space of all possible relational patterns. Understanding this trinity illuminates what transformers actually do: they cycle between these three levels of infinity to transform discrete symbols into meaning.
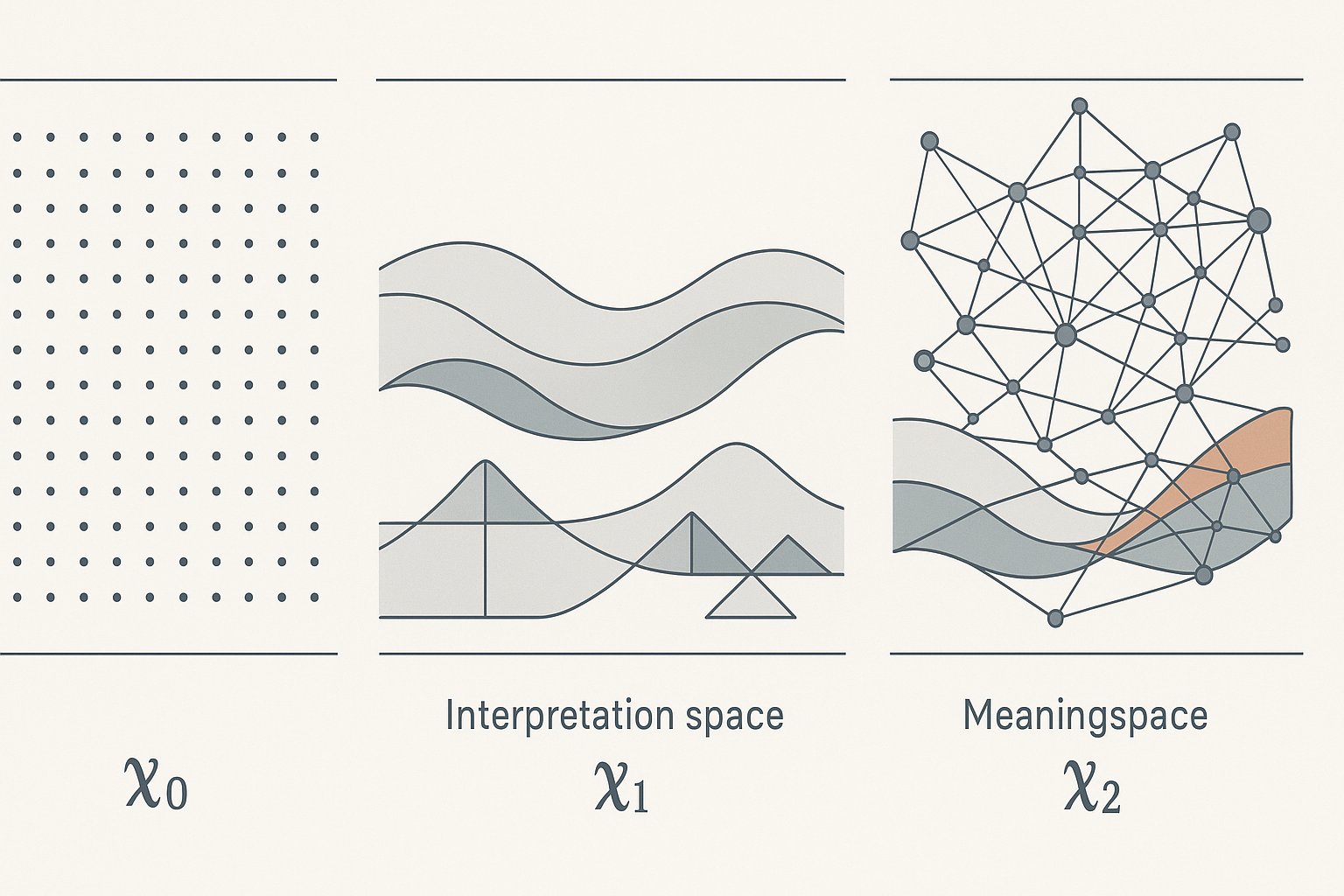
Factspace, Interpretation Space, Meaningspace
The first infinity defines factspace—the domain of discrete, countable facts. Here live the atomic units of information: specific tokens, individual data points, enumerable truths. Facts can be listed, counted, verified. They exist as distinct entities with clear boundaries. In transformer architecture, this manifests as vocabulary indices, position encodings, and ultimately, the discrete token predictions the model produces.
The second infinity creates interpretation space—the continuous field where discrete facts become embedded in geometric relationships. This is where the actual computation happens. Embedding matrices map discrete tokens into continuous vectors. These vectors can be rotated, scaled, interpolated. The continuity of this space enables smooth navigation between concepts, gradual transformation of meaning, and the geometric operations described in Geometry First, Statistics Second. Every weight in a transformer defines a specific trajectory through this interpretation space.
The third infinity opens into meaningspace—the realm of all possible relationships between interpretations. As explored in Welcome to Meaningspace, this isn't just another level of measurement but a fundamentally different kind of space. Each attention head reaches into a different fragment of this relational infinity, extracting different patterns of connection. Meaningspace contains not just where things are or how they measure, but all the ways they can relate, transform into each other, and create significance through their interactions.
The Computational Cycle
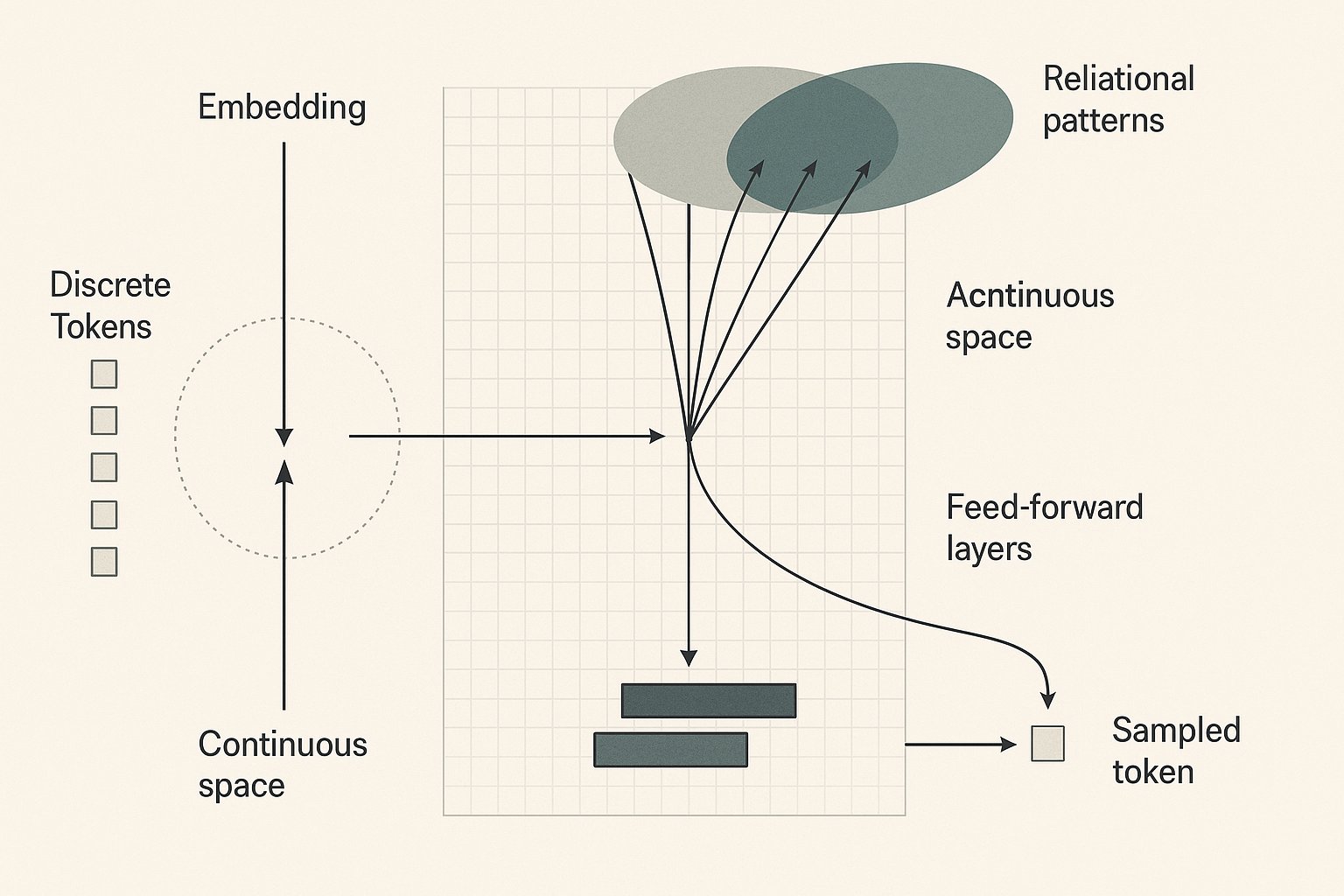
What actually happens when a transformer processes text is a precise journey through these three infinities. Input tokens begin as discrete selections from ℵ₀. The embedding layer lifts these into the continuous space of ℵ₁, where each token becomes a vector in high-dimensional space. This transition from discrete to continuous enables the smooth geometric operations that follow.
Attention mechanisms then access ℵ₂. Each attention head implements a different relational function—a different way of determining which vectors should influence each other and by how much. These aren't just measurements in continuous space; they're functions that define relationships between positions in that space. Multi-head attention samples multiple fragments of meaningspace simultaneously, each head capturing different relational patterns.
The journey reverses as the model produces output. The rich relational patterns from ℵ₂ project back down to continuous logit vectors in ℵ₁. The softmax operation maintains this continuity while preparing for the final discretization. Sampling collapses this continuous distribution back to a discrete token in ℵ₀. The cycle completes: discrete to continuous to relational and back to discrete.
Invariance and Composition
Through the layers of a transformer, different fragments of meaningspace compose hierarchically. Early layers might capture syntactic relationships, while deeper layers access semantic and pragmatic patterns. The residual connections preserve information across these transformations, allowing patterns that remain stable across multiple relational views to survive and strengthen.
This process resembles Noether's theorem in physics: the output represents semantic invariances that survive transformation through multiple relational perspectives. What emerges in the final logits isn't just a prediction but the compositional invariant of all the relational fragments applied throughout the network. The model doesn't retrieve facts; it discovers what remains stable across many different ways of relating the input elements.
Different architectures manipulate this trinity in different ways. Mixture of Experts creates multiple parallel interpretation spaces in ℵ₁, each accessing different fragments of ℵ₂. Quantization reduces the resolution of ℵ₁ while preserving essential pathways to ℵ₂. The success of these techniques demonstrates that what matters isn't perfect representation at any single level but preserving the essential mappings between levels.
Implications for Intelligence
Understanding these three infinities reframes what artificial intelligence systems actually do. They don't store and retrieve facts from ℵ₀. They don't just measure distances in ℵ₁. They navigate the relational patterns of ℵ₂, discovering invariances that bridge between discrete facts and infinite meanings.
This trinity suggests why scaling works: larger models can access more fragments of meaningspace, compose more relational perspectives, and discover subtler invariances. But it also suggests limits—no finite system can exhaust ℵ₂. There will always be new relational patterns, new ways of connecting interpretations that haven't been explored.
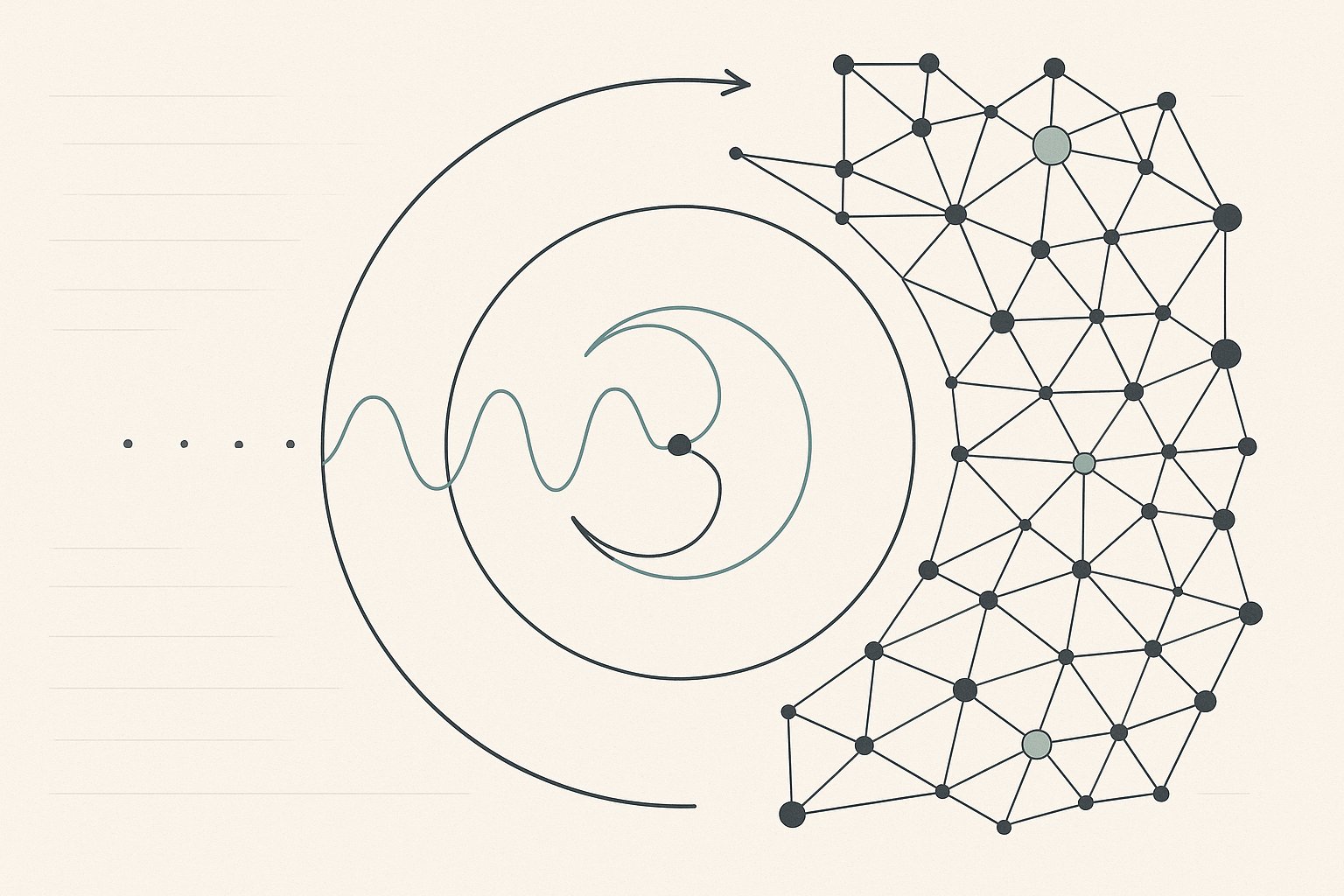
The semantic binary between discrete counting and continuous interpolation means nothing can exist between ℵ₀ and ℵ₁—they represent fundamentally different modes of being. But the transition from ℵ₁ to ℵ₂ opens into inexhaustible richness. Every possible way of relating, transforming, and creating meaning exists in this highest infinity. Transformers are machines for navigating this space, discovering through their learned geometries which relational patterns matter for the tasks we set them.